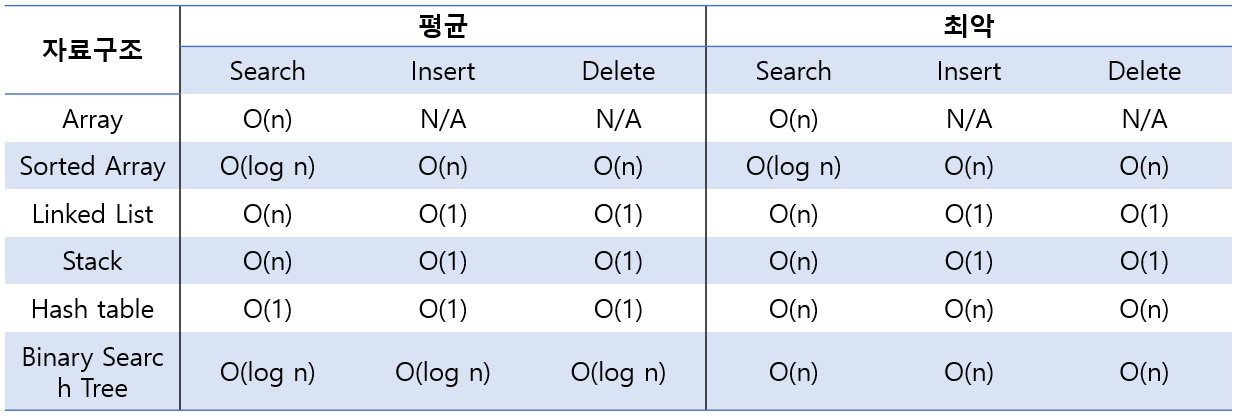
시간 복잡도

2020-02-18

해당 Post는 시간 복잡도에 대해 정리한 파일입니다.

시간복잡도(Time Complexity)

시간복잡도의 가장 간단한 정의는 알고리즘의 성능을 설명하는 것입니다.

점근적 표기법은 다음 세가지가 있는데 시간복잡도를 나타내는데 사용됩니다.

점진적 표기법 구성

  • 최상의 경우 : 오메가 표기법 (Big-Ω Notation)
  • 평균의 경우 : 세타 표기법 (Big-θ Notation)
  • 최악의 경우 : 빅오 표기법 (Big-O Notation)

세타 표기법을 사용하면 정확하고 좋지만 평가하기가 까다롭습니다.

일반적으론 최악의 경우인 빅오를 사용하는데 최악의 경우를 판단하여 예측하기 쉽기 때문입니다.

빅오 표기법(Big-O)

빅오 표기법은 불필요한 연산을 제거하여 알고리즘분석을 쉽게 할 목적으로 사용됩니다.

Big-O로 측정되는 복잡성에는 2가지가 있습니다.

첫째, 시간복잡도는 알고리즘에 사용되는 연산횟수의 총량

둘째, 공간복잡도는 알고리즘에 사용되는 메모리 공간의 총량

공간복잡도는 메모리의 발전으로 중요도가 낮아졌습니다.

시간복잡도에서 중요하게 보는것은 가장큰 영향을 미치는 n의 단위입니다.

  • O(1) : 입력자료의 수에 관계없이 일정한 실행시간을 갖음
  • O(logn) : 입력자료의 수에 따라 시간이 흐를수록 시간이 조금씩 증가
  • O(n) : 입력 자료의 수에 따라 선형적인 실행 시간이 걸리는 경우 - 입력자료마다 일정 시간 할당
  • O(nlogn) : 큰 문제를 일정 크기 갖는 문제로 쪼개고(logn+logn+ .. + logn) 다시 그것을 모으는 경우
  • O(n^2) : 이중 루프내에서 입력 자료를 처리할 때
  • O(n^3) : 삼중 루프 내에서 입력자료 처리할 때

시간 복잡도가 빠른 순

O(1) > O(logn) > O(n) > O(nlogn) > O(n^2) > O(n^3) > O(2^n) > O(n!)

정렬알고리즘에서의 시간복잡도

My Image

자료구조에서의 시간복잡도

My Image