위 문제는 Programmers 멀쩡한 사각형 문제에 관한 설명입니다.

문제

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다.

종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다.

이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데,

누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다.

그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다.

새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.

가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

제한 사항

• W, H : 1억 이하의 자연수

입출력 예 설명

입출력 예 #1

가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다.

원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.

class Solution {   
    public static long GCD(long num1, long num2){
        if(num2 == 0) return num1;
        else return GCD(num2, num1 % num2);
    }
    
	public long solution(int width,int height) {
        long w = (long)width;
        long h = (long)height;
        long total = w * h;
        long sub = w + h;
        long gcdValue = GCD(w,h);
        
        if(gcdValue > 1) sub -= gcdValue; 
        else sub -= 1;
        
        return total - sub;
	}
}

이번 문제를 풀기 위해 규칙을 찾아야 했습니다.

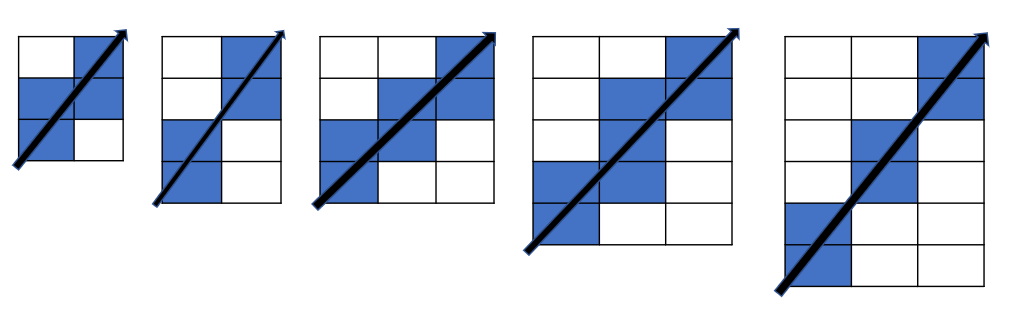
그림을 보았을 때,

1번째 가로 2, 세로 3 지나는 칸 = 4

2번째 가로 2, 세로 4 지나는 칸 = 4

3번째 가로 3, 세로 4 지나는 칸 = 6

4번째 가로 3, 세로 5 지나는 칸 = 7

5번째 가로 3, 세로 6 지나는 칸 = 6

언뜻 보면 잘 모를 수 있습니다.

그러나 깔끔하게 대각선으로 꼭지점들을 지나는 녀석들은 신기하게도

가로 + 세로 - (가로와 세로의 최대공약수)의 패턴을 가집니다!

그외의 녀석들도 가로 + 세로 - 1 이라는 값을 가지게 됩니다.

따라서 이번 문제에서는 최대공약수를 구할 수 있고, 저 규칙을 찾아낼 수 있는가가 관건 이었습니다.

멀쩡한 사각형