컴퓨터 네트워크를 공부하면서 정리를 한 내용들 입니다.

-참고 K-mooc 부산 대학교 유영환 교수님 : 컴퓨터 네트워크 강의

---

Dijkstra’s Algorithm Example

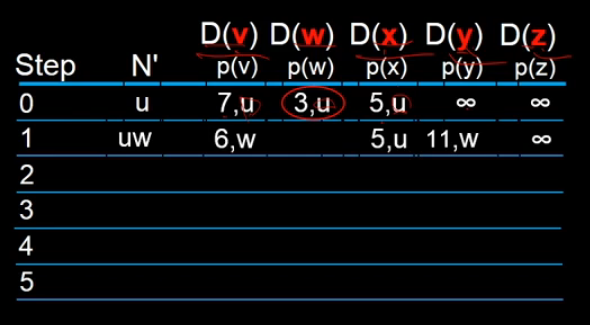
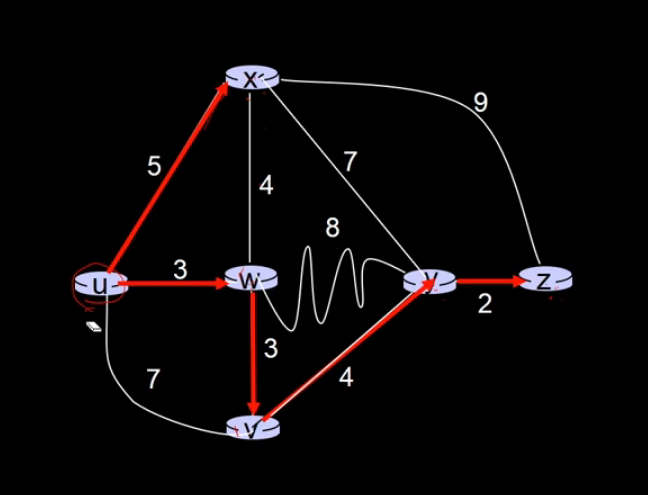
지금 주어진 그래프는 6개의 라우터를 가진채로 세팅이 됩니다.

v, w, x로의 비용은 7, 3, 5 이렇게 설정이 되고,

그 뒤에 u 라는 것은 v, w, x에 오기 위해서

이전에 어떤 node를 거쳤는가 하는 것입니다.

바로 직전에 u에서 직접 왔기 때문에 v, w, x의 직접 노드는

u가 되어서 아래의 표와 같이 표현이 됩니다.

y와 z는 현재 직접 연결이 없기 때문에 무한대가 됩니다.

여기서 직접 경로가 연결 되어 있는 node들.

v와 w, x 중에서 w로 가는 링크의 비용이 가장 작습니다.

그 말은 w는 다른 링크를 한 번이라도 거치게 되면

3보다는 더 적은 비용으로 갈 수가 없다는 뜻이 됩니다.

반면에 다른 node들은,

다른 라우터들은 w를 거쳐서 갈 때 더 적은 비용으로

도달 할 수 있는 가능성도 있습니다.

그래서 v, w, x 중에 가장 작은 비용을 가진

w를 먼저 선정 해서 최소 비용 경로를 확정 합니다.

그 뒤에 하는 일은 이 w 외의 다른 node들 v, x, y, z에 대해서

w를 거쳐 갈 때 현재 알고 있는 비용보다

더 적은 비용으로 갈 수 있는지를 살펴 보는 것입니다.

그러면 v같은 경우에는 w를 거치면 3+3이 되어서 6이 되고,

비용이 현재 알고있는 7에서 6으로 줄어 들어야합니다.

x는 3+4가 되니까 7이 되고 현재 알고 있는 5 보다는 더 큰 값이 됩니다.

이 값은 무시합니다.

다음에 y로는 현재 무한대이지만,

w에서 y로의 직접 링크인 8의 비용을 가진 직접 링크가 있기 때문에

3+8을 하면 11이 됩니다.

그리고 z는 w에서 직접 링크가 없기에 여전히 무한대로 남습니다.

여기 까지의 결과가 아래의 표와 같이 표현이 됩니다.

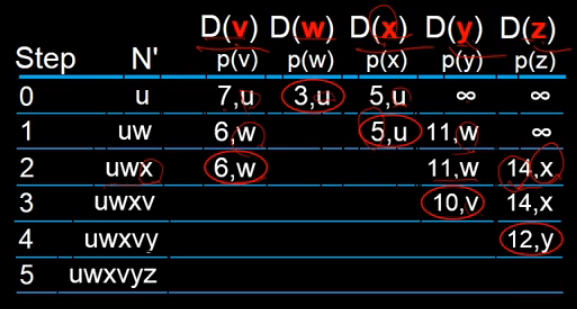
그러면 1번 라인에서 가장 최소 비용 경로를 갖는 node는 x입니다.

x가 최소 비용 경로가 확정 된 집합되어 선택됩니다.

아직 선택 되지 않은 최소 비용 경로가 계산 되지 않은

v나 y나 z에 대해서 최소 비용 경로가 갱신 되는지를 살펴 봅니다.

현재 v는 6이라는 값을 갖고 있는데 x를 거친다고 해서

그 비용이 줄어들지는 않습니다.

오히려 x는 v로의 직접 경로가 없기 때문에 무한대로 계산 합니다.

y는 x에서 직접 링크가 있기는 하지만 5+7을 하게 되면

12가 되고 현재 알고 있는 11 보다는 큰 값입니다.

그래서 갱신이 되지 않을 것이고,

z는 5+9가 되어 14로 현재 무한대 보다는 작은 값이기에 갱신됩니다.

v로의 최소 비용 경로나 y로의 최소 비용 경로는 갱신되지 않지만

z로는 14로 갱신되면서 직전 node가 x이다 이렇게 계산 됩니다.

이제 2번 라인에서 가장 최소 비용 경로를 가지는 destination은 v입니다.

그러면 v가 선택이 되어서 들어가고

혹시 y나 z로의 최소 비용 경로가 갱신 되는지를 살펴 봅니다.

현재 y로 가는 경로의 최소 비용은 w를 거쳤을 때 11이지만,

v를 거치면 3+3+4 하면 10이 되어 갱신이 됩니다.

v는 z로 직접 경로가 없기 때문에 이 때는 무한대로 계산되고,

그러면 이것은 갱신이 되지 않습니다.

그래서 이 과정을 반복하고 나면 모든 node들이 여기 포함이 됩니다.

그러면 이렇게 해서 알고리즘은 끝이 나고

그 다음 하는 일은 계산 된 표에서 마지막에 포함 된 z를 통해서

모든 경로를 거쳤다는 것을 확인할 수 있습니다.

이 경로들을 그림으로 나타낸 것이

빨간색으로 그려 진 tree가 u에서부터

모든 node로 가는 가장 짧은 path를 이은 tree가 되고,

u는 이 경로를 따라서 전송을 하게 되면

각 node로 최소 비용 경로로 전달 할 수 있게 됩니다.

---