BOJ 11049
2021-01-24
위 문제는 백준 사이트의 알고리즘 11049 문제에 관한 설명입니다.
문제
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다.
행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에
행렬의 곱 ABC를 구하는 경우를 생각해보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는
5×3×2 + 5×2×6 = 30 + 60 = 90번이다. - BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는
3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때,
모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오.
입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
입력
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
출력
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다.
정답은 231-1 보다 작거나 같은 자연수이다.
또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같다.
package DP2;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ11049 {
static int[][] matrix;
static int[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(reader.readLine());
matrix = new int[N][2];
dp = new int[N][N];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(reader.readLine());
matrix[i][0] = Integer.parseInt(st.nextToken());
matrix[i][1] = Integer.parseInt(st.nextToken());
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
System.out.println(solve(0, N - 1));
}
public static int solve(int start, int end) {
if (start == end)
return 0;
if (dp[start][end] != Integer.MAX_VALUE) {
return dp[start][end];
}
for (int i = start; i < end; i++) {
int cost = solve(start, i) + solve(i + 1, end) + matrix[start][0] * matrix[i][1] * matrix[end][1];
dp[start][end] = Math.min(dp[start][end], cost);
}
return dp[start][end];
}
}
이번 문제는 동적프로그래밍 문제 였습니다.
예제를 보고 solve 함수의 동작을 하나씩 따라가 보았습니다.


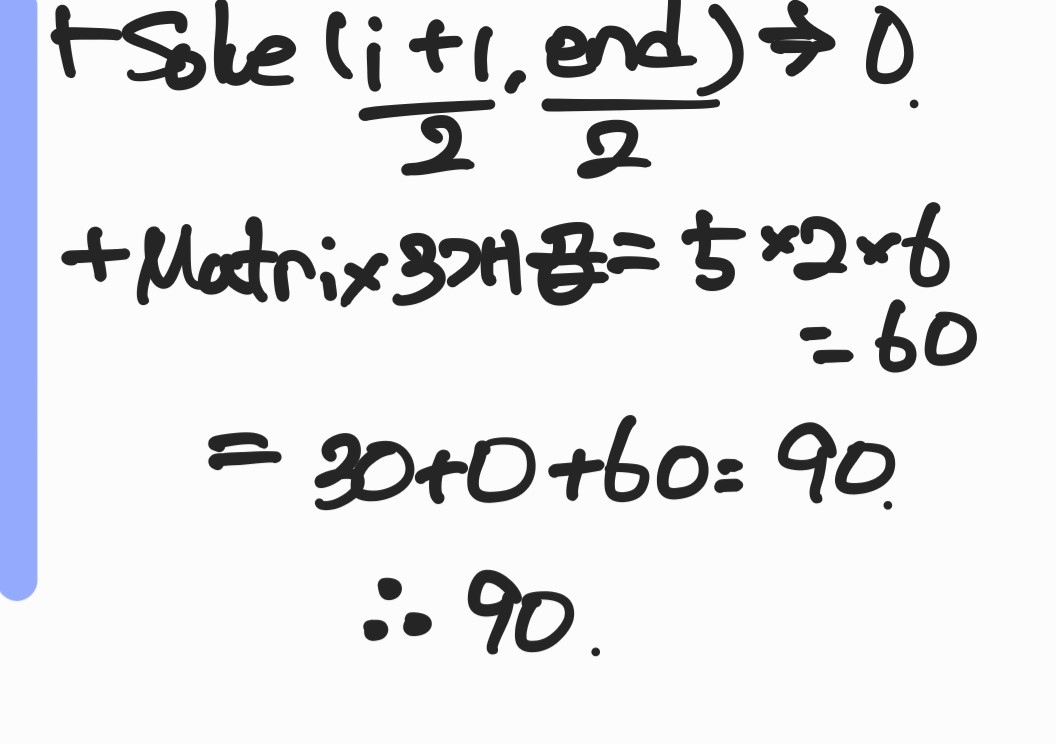
이 과정을 거치게 되면 결과적으로 dp[0][n-1]에는 코스트들중 최소값이 뽑히게 됩니다.